DeepRL - Rotational Inverted Pendulum

The field of Deep Reinforcement Learning brought us events like DeepMind's AlphaGo win against the best human Go players Lee Sedol (South Korea) and Ke Jie (China). The Atlantic

The summary of the difficulty of this problem is: "The number of possible board configurations in Go is more than the number of atoms in the universe."

What is reinforcement learning?

A reinforcement learning agent learns from an environment which specifies the objective in terms of a reward function. The agent updates its behavior to maximize the cumulative rewards gathered from the environment each episode. Maze navigating agent - Wikipedia

In this maze navigating example the reward function can be specified as simply as +1 when the maze is completed and -0.01 for every decision made. The reward function is critical to RL, in that it is the sole way to define a goal for the agent.

Terminology

Heavily looted from Google's ML Glossary.

Agent: Entity that uses a policy to maximize expected return gained from transitioning between states of the environment.

Observations: The set of information about the environment that the agent uses to make decisions and learn.

Action: The action which the agent takes based on its observations.

Reward: The signal provided by the environment that the agent uses to evaluate the successfulness of a given policy in an environment.

Episode: One attempt by the agent to navigate the environment.

Training: Using the history of an episode (observations, actions, collected rewards) to update the policy towards increased rewards.

The Rotational Inverted Pendulum Environment

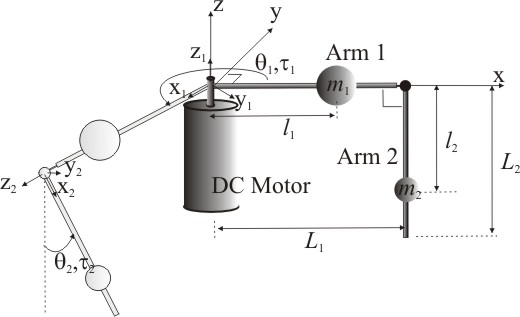
My junior year of college in class called "Systems Engineering Lab" we spent the duration of a semester solving the Rotational Inverted Pendulum (aka the Furuta Pendulum).

"The Furuta pendulum, or rotational inverted pendulum, consists of a driven arm which rotates in the horizontal plane and a pendulum attached to that arm which is free to rotate in the vertical plane." - Wikipedia Futura Pendulum - Wikipedia

Here's a video of it in action for more clarity:

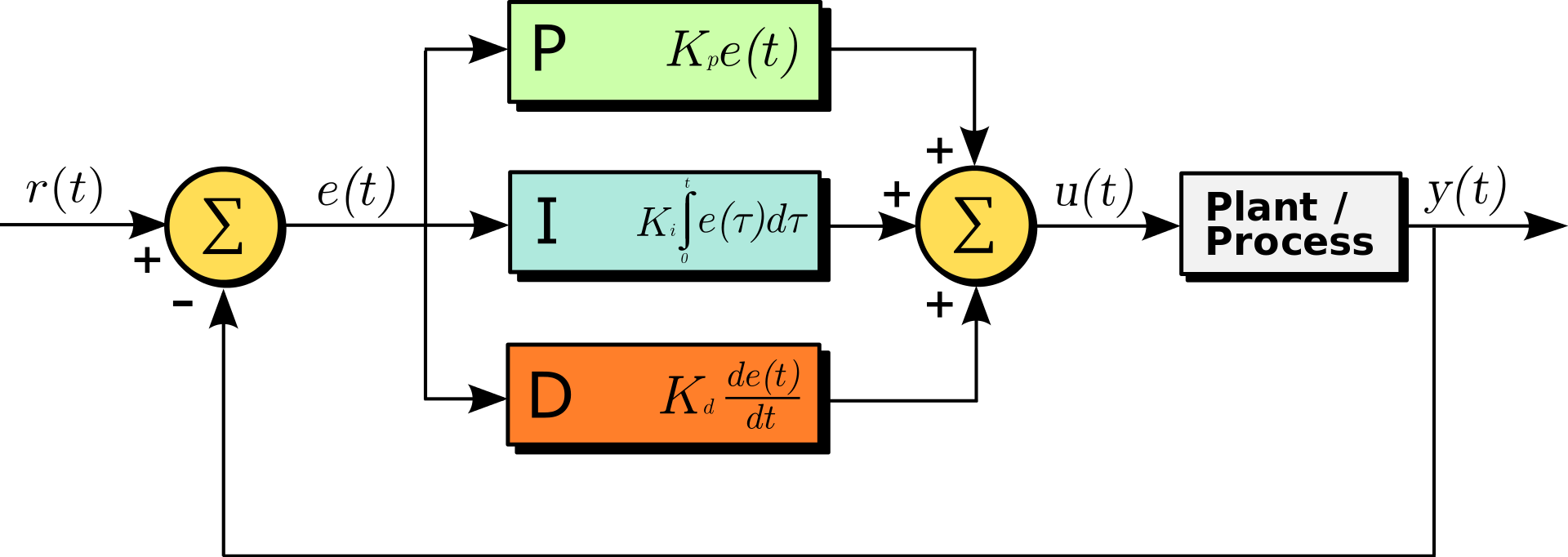
We used PID controllers to solve this problem, and the gist of these is fairly simple.

Create an error signal to drive the controller. This is the difference between your desired value and the actual value

$Error(\theta) = desired - \theta$

Now create three terms from this error signal

$P = kP * Error(\theta)$

$I = kI * \int Error(\theta)d\theta$

$D = kD * \frac{d}{d\theta}Error(\theta)$

Then finally create the control signal by summing these three. Wikipedia

Then the three weights are tuned such that the resulting control signal produces reliable results. The intuitive way to think about this is: for a given error signal there is a way to combine the rate of change/speed of the error signal (kD term) with the actual error signal (kP term) with the duration of error (kI term) such that a reliable control signal is produced. I have a degree in calculating these terms, but in practice, trial and error is your friend.

For the Futura Pendulum this involved several of these controllers feeding into each other with a PID dealing with the action space when the pendulum was at the top of rotation. PID controllers are the basis of much of the worlds control systems due to their simplicity, predictability and (relative) ease of compute. Our PID Tuned Futura Pendulum

Applying Deep RL

I rebuilt this environment in Unity with Nvidia PhysX for the physics and link simulations and Unity's in-house ML-agents framework to deal with Deep RL training. Environment The coordinate space is defined as a vertical pendulum is at $\theta = 0$ and each degree counter clockwise is +1 and each degree clockwise is -1.

At the beginning of each episode we spawn the end-effector somewhere in the range (-180, 180).

Optimal rewards range from (-1 to 1) so our per-step reward function is defined as:

$if |\theta| < 90: Reward = (90-|\theta|)^2/(90^2)$

$else: Reward = -0.01$

We collect the following observations from a given robot every step.

1. Angular velocity of the rotating arm
2. Angular velocity of the end-effector
3. Angular position of the end-effector theta

The Action we take in this environment based on these observations is a value ranging from -1 to 1 corresponding to how much torque to apply to the base axle.

Now we batch up these training robots into a set of 9 to a) make training more efficient and b) ensure that the observations we collect from the environment for training are sufficiently diverse. Note that these 9 robots share 1 brain. This brain can be thought of simply as a decision factory of which you ask "here are the observations of the current state of this robot, please give me an action to take". Batch Environment

The Algorithm

We are going to train this agent using an algorithm from OpenAI (Musk's AI research venture) called PPO which is based on TRPO and other On-Policy Deep RL algorithms. _I'm going to euphemize the work of these very bright people in an effort to make this somewhat more approachable. _

The deep in "Deep RL" means that some portion of the decision is made by a neural network. Neural networks are the basis of most of the field of machine learning and can be thought of as a generalized logistic regression. In other words, a neural network is trained to be a function where:

$F(inputs) = outputs$

For the algorithm we're using there are two main networks we will be training.

(1) Value network

Convert observations -> Predicted reward for a given action

$F(Observations) = Predicted\ Reward$

Trained on the history of a given episode to more accurately predict the outcome of the episode.

(2) Policy network

Convert observations -> actions

$F(Observations) = Action$

Trained on each iteration to increase the likelihood of selecting actions with a higher expected reward (from the value network).

The intuitive need for the value network comes down to the ability of the policy network to plan and decrease the sparsity of reward signals. The value network allows the agent to try to estimate the value of an action on end result of an episode: swinging the pendulum from -200 -> -180 may not provide a direct reward from the environment, but the agent will start to understand that this action is one that would take it towards future rewards.

The goal is to train both of these networks such that the policy maximizes the reward (upright pendulum).

Results

20k Steps

30k Steps of Training They are very dumb.

200k Steps

200k Steps of Training Starts to understand the basic goal of swinging the pendulum to the top. Now its off to the races.

2M Steps

2M Steps of Training The agent is being a good boy.

Environment rewards over time

Depending on hyper-parameters (training parameters), agents tend to converge to a reward of ~600/episode at slightly different speeds. 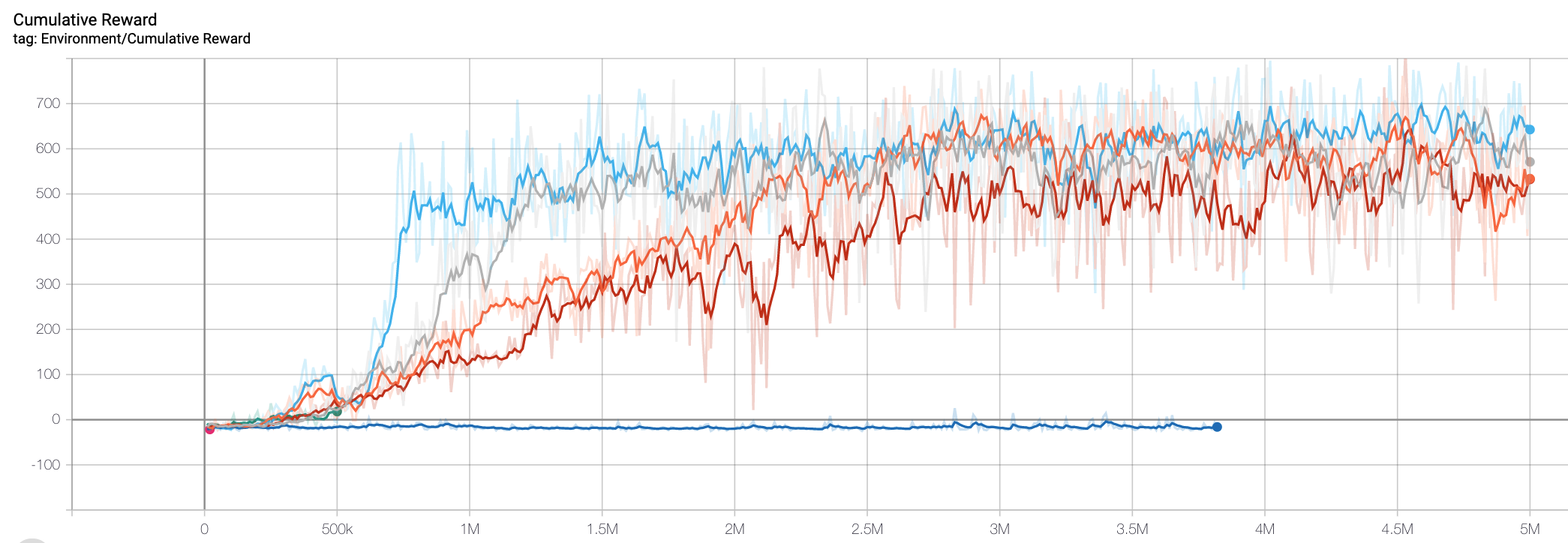Environment rewards over time For the same training runs here is the "loss" of the value function. This corresponds to the accuracy of the predictions by the value network about the expected reward of the episode for a given set of observations (loss = |actual - predicted|; high loss -> low accuracy). 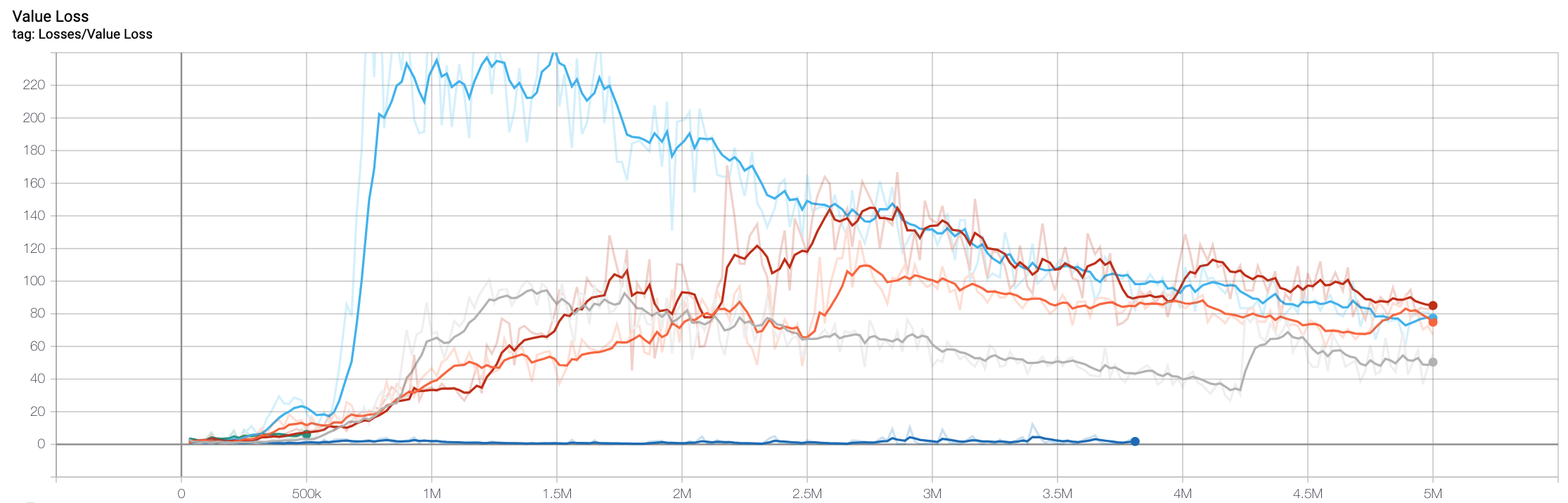Value Loss

Future

This article focused on a high-level overview of these very cool algorithms, but if you're reading this and interested in more depth, please let me know.

The initial goal of this work was to see if the networks learned in this simulation could be transfer-learned onto a live robot to decrease real-world training time dramatically (which can't be parallelized, nor sped up). I currently don't have a live version of this robot, but may build one down the line. If I do approach this I will likely need to rebuild the physics of the unity simulation using the actual equations of motion rather than relying on the accuracy of Nvidia PhysX.

Anyways, its time for me to spend time on something else, thanks for reading!

Source Code

• Github